СОДЕРЖАНИЕ ПРОГРАММЫ МЕТА-ШКОЛЫ «ГРАНИ» ПО МАТЕМАТИЧЕСКОМУ ТЕМАТИЧЕСКОМУ МОДУЛЮ
Приоритетные направления развития:
· математическая грамотность
· информационная грамотность
· глобальные компетенции
Пояснительная записка
1. Определение математической грамотности
«Математическая грамотность – это способность человека формулировать, применять и интерпретировать математику в разнообразных контекстах.
Она включает математические рассуждения, использование математических понятий, процедур, фактов и инструментов, чтобы описать, объяснить и предсказать явления. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые необходимы конструктивному, активному и размышляющему гражданину. В уточненном определении математической грамотности говорится о том, что она включает умение работать с математическими инструментами. К ним отнесены физические и цифровые устройства, присущие технологии 21 века, использование которых стало общепринятым и продолжает расширяться. Очевидно, что владение этим умением является необходимым условием успешности современного человека.
С 2012 года часть математических заданий в международных исследованиях по-прежнему предлагалась и выполнялась на бумаге, а часть заданий предлагалась на компьютере, и свои ответы ученики вводили в компьютер. Задания, которые предлагались на компьютере, позволили расширить область предлагаемых для анализа ситуаций, математических инструментов и данных, например, за счет включения наборов пространственных геометрических конструкций, виртуальных измерительных инструментов, различных наборов объемных статистических данных.
2. Области исследования математической грамотности
В основу организации области исследования математической грамотности положены три пересекающихся аспекта:
· математическое содержание, которое используется в тестовых заданиях;
· контекст, в котором представлена проблема;
· математические мыслительные процессы, которые описывают, что делает ученик, чтобы связать этот контекст с математикой, необходимой для решения поставленной проблемы.
Для описания деятельности при решении задач предлагаются три глагола
· формулировать;
· применять;
· интерпретировать.
Они явно отражают основные виды деятельности при решении проблем посредством использования математики. Они указывают на три мыслительных процесса, в которые, как правило, будут вовлечены учащиеся при активном участии в решении проблем:
· формулировать ситуацию математически;
· применять математические понятия, факты, процедуры размышления;
· интерпретировать, использовать и оценивать математические результаты.
Формулировать ситуации математически (formulating situations mathematically) включает способность распознавать и выявлять возможности использовать математику, принять имеющуюся ситуацию и трансформировать ее в форму, поддающуюся математической обработке, создавать математическую модель, отражающую особенности описанной ситуации; определять переменные, размышлять и понимать условия и допущения, облегчающие подход к проблеме или ее решение.
Применять математику (employing mathematics) включает способность применять математические понятия, факты, процедуры, рассуждения и инструменты для получения решения или выводов. Эта деятельность включает выполнение математических процедур, необходимых для получения результатов и математического решения (например, выполнять действия с алгебраическими выражениями и уравнениями или другими математическими моделями, анализировать информацию на математических диаграммах и графиках, работать с геометрическими формами в пространстве, анализировать данные). Работать с моделью, выявлять закономерности, определять связи между величинами и создавать математические аргументы.
Интерпретировать (interpreting mathematics) включает способность размышлять над математическим решением или результатами, интерпретировать и оценивать их в контексте реальной проблемы. Эта деятельность включает перевод математического решения в контекст реальной проблемы, оценивание реальности математического решения или рассуждений по отношению к контексту проблемы. Этот процесс охватывает и интерпретацию, и оценку полученного решения или определение того, что результаты разумны и имеют смысл в рамках предложенной ситуации. При этом может потребоваться разработать объяснения или аргументацию с учетом контекста проблемы
Фундаментальные математические способности, которые являются неотъемлемой частью математической грамотности:
· передача сообщений/информации;
· математизация;
· представление;
· рассуждения и аргументация;
· разработка стратегии решения проблемы;
· использование символьного, формального или технического языка и операций;
· использование математических инструментов.
На рисунке 1 представлена модель математической грамотности .
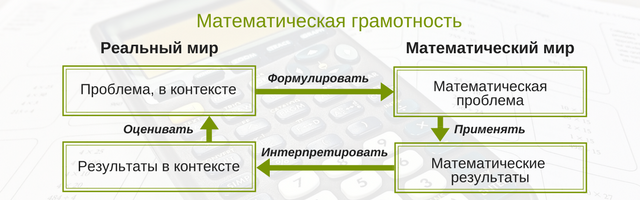
Рис. 1. Модель математической грамотности
3. Области оценки математической грамотности
В международных исследованиях в основу организации структуры математического содержания, которым должен обладать грамотный человек для решения разнообразных проблем, положен особый подход. Этот подход отличается от подхода, характерного для целей обучения математике и школьных программ – структурирование по содержательным линиям и математическим темам.
В исследовании математическое содержание распределено по четырем категориям:
· пространство и форма;
· изменение и зависимости;
· количество;
· неопределенность и данные.
Эти категории охватывают основные типы проблем, возникающих при взаимодействиях с повседневными явлениями. Именно из тематики содержания, охватываемого этими идеями, извлекаются соответствующие вопросы содержания, используемые для решения поставленной проблемы:
· Изменение и зависимости – задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом;
· Пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу;
· Количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относится к курсу арифметики;
· Неопределенность и данные – область охватывает вероятностные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности.
4. Дескрипторы оценки достижений учащихся в математическом модуле
МГ 1. Исследует ситуацию
1 – простую, знакомую, по алгоритму;
2 - частично знакомую, не алгоритмизированную;
3 - сложную проблемную с большой долей неопределенности.
МГ 2. Использует знания в нетипичных контекстах.
0 – нет;
1 –да.
МГ 3. Связывает и использует информацию из разных источников.
0 – нет;
1 –да.
МГ 4. Работает с информацией.
1 – представленной в текстовой форме;
2 - представленной в различных формах (текста, таблицы, диаграммы столбчатой или круговой, схемы, рисунка, чертежа с обозначением видимых и невидимых элементов геометрической фигуры) в контексте конкретной проблемы;
3 - свободно преобразовывает и переходит от одной формы к другой.
МГ 5. Применяет интуицию и понимание наряду с владением математическими символами, операциями и зависимостями при разрешении незнакомых проблемных ситуаций
0 – нет;
1 –да.
МГ 6. Размышляет над своими действиями, формулирует и комментирует, почему они были использованы в данной ситуации
0 – нет;
1 –да.
МГ 7. Удерживать условия задания в процессе решения;
0 – нет;
1 –да.
МГ 8. Осуществляет самоконтроль за своими действиями;
0 – нет;
1 –да.
II. Содержание тем в математических модулях программы «Грани».
Тема 2019-2020 года «Человек мира»
|
№ темы |
Содержательная линия |
Кол-во часов |
Возможные формы и методы |
|
5 класс (Алиева Гюнай) |
|
1 |
Тише едешь – дальше будешь |
1 |
Урок-поиск. Составление географической картины государства языком математики, то есть цифрами.
|
|
2 |
Копейка рубль бережет |
1 |
Урок-лекция. Классическая форма проведения урока, в которой ученики узнают немного об экономики государства с математической точки зрения. Решение практически применимых жизненных задач, с которыми ежедневно сталкиваются взрослые, и даже дети. |
|
3 |
Кто путешествует тот, познает |
1 |
Кейс-метод. Главное его предназначение – развивать способность находить решение проблемы и учиться работать с информацией. При этом акцент делается не на получение готовых знаний, а на их выработку. Учащиеся научатся находить рациональные и оптимальные пути решения проблемы, которой окажется планирование длительной поездки при определенных условиях. |
|
4 |
Хочешь есть калачи – не сиди на печи |
1 |
Урок-игра. |
|
5 |
Реставрация достопримечательности |
1 |
Стратегическая деловая игра. Данный формат урока позволит сымитировать процесс, который требует разрешения, он позволяет учащимся быстро и качественно закрепить знания и навыки, которые они получают. |
|
6 класс (Алиева Гюнай) |
|
1 |
Тише едешь – дальше будешь |
1 |
Урок-поиск. Составление географической картины государства языком математики, то есть цифрами.
|
|
2 |
Копейка рубль бережет |
1 |
Урок-лекция. Классическая форма проведения урока, в которой ученики узнают немного об экономики государства с математической точки зрения. Решение практически применимых жизненных задач, с которыми ежедневно сталкиваются взрослые, и даже дети. |
|
3 |
Кто путешествует тот, познает |
1 |
Кейс-метод. Главное его предназначение – развивать способность находить решение проблемы и учиться работать с информацией. При этом акцент делается не на получение готовых знаний, а на их выработку. Учащиеся научатся находить рациональные и оптимальные пути решения проблемы, которой окажется планирование длительной поездки при определенных условиях. |
|
4 |
Хочешь есть калачи – не сиди на печи |
1 |
Урок-игра. |
|
5 |
Реставрация достопримечательности |
1 |
Стратегическая деловая игра. Данный формат урока позволит сымитировать процесс, который требует разрешения, он позволяет учащимся быстро и качественно закрепить знания и навыки, которые они получают. |
|
7 класс (Чиглинцева Татьяна) |
|
1 |
Единицы измерения. |
1 |
Вычислительный эксперимент (перевод значений своего роста, возраста и т.д. в единицы измерения выбранной страны, современные или старинные). |
|
2 |
Геометрические формы в архитектуре. Расчет прочности сооружений. |
1 |
Математическое иследование. (за основу идеи взято: особенности архитектуры стран мира, симметрия – царица архитектурного совершенства). |
|
3 |
Выбор формы и конструкции, чертеж или схема макета здания |
1 |
Математическое моделирование. (в стиле выбранной страны или достопримечательности этой страны) |
|
4 |
Создание макета. (возможно, в электронном варианте) |
1 |
Математическое моделирование. |
|
5 |
Проектируем виртуальный город.. (объединение макетов в единый город, возможно, виртуальный) |
1 |
Математическое моделирование Презентация моделей |
|
8 класс (Чиглинцева Татьяна) |
|
1 |
1.Интересная статистика.
Анализ статистических данных о стране, построение графика успешности/популярности страны на основе этих данных. |
1 |
Ролевая игра «Статистическое бюро» |
|
2 |
Транспорт в цифрах
Решение проблемных задач |
1 |
Интеллект-марафон «Поехали!» |
|
3 |
Выгодный шопинг.
Составление расчетной таблицы покупок |
1 |
Деловая игра «Математика для «блондинок». Создание интеллект-карты
|
|
4 |
Рейтинг в процентах.
Создание диаграммы конкурентоспособности страны |
1 |
Деловая игра «Мировой рейтинг»
Анализ, визуализация, аргументация |
|
5 |
Формула успеха.
Подведение итогов, перспективы дальнейшего развития, составление логической формулы успеха страны, на основе собранных и обработанных данных |
1 |
Математическое моделирование и прогнозирование. |